지금까지의 소비자 선택이론과 그 응용을 보았을 때, 소비자들의 선택은 확실한 상황과 비교가 가능한 상황에서의 소비자 선택에 대한 가정과 모형들을 이론화한 것들을 보았다.
하지만 현실에서는 어떠한 소비를 하려할 때 결과가 불확실한 경우가 많다.
한가지 예를 들어 당신이 복권을 구입하고자 할때 복권 구매에 대한 효과를 구매 당시 당신은 예측할 수 있는가?
이러한 불확실한 상황아래에서 소비자가 어떤식으로 선택하는지에 대한 연구를 진행한 분야가 기대효용이론이다.

위험에 대한 태도 분류
사실 사람은 불확실한 상황을 상당히 싫어하는 경우가 많다.
확실하게 성공할 수 있는 방법이 있다면, 또 확실히 좋은 선택을 할 수 있다면 어느누가 불확실한 선택을 하려할까?
하지만 애석하게도 현실은 그렇지 못하다.
살다보면 어리석은 선택을 하는 경우도 있고 나중에 내가 왜 그런 선택을 했을까 후회한 적도 한두번이 아니다.
특히 인생이 내 마음대로 되지 못하는 이런 상황.
그렇다면 우리는 어떻게 해야 불확실성을 줄이고 좋은 선택을 할 수 있을지에 대한 고민이 당연히 많아지게 될 것이다.
이러한 불확실성에 대한 상황은 위험요소에서 발생한다.
위험과 불확실한 상황에 대해서 기피하는 성향이 있긴하지만 아이러니하게도 위험요소가 높은 대신 만약 그에 따른 기대효용이 높다면, 이를 선택하려는 소비자들도 상당수 있다.
이러한 위험과 그에 따른 효용의 관점에서 관찰하다 보면 위험에 대한 사람의 태도는 또한 다양하다.
첫째는 '위험기피자' 이다.
위험이 비재화라고 표현되기도 하는데, 이런 상태는 "기대효용(효용의 기대치)이 기대금액의 효용보다 작은 경우" 이다.

둘째는 '위험중립자'이다.
위험이 중립재라고 표현되기도 하는데, 이런 상태는 "기대효용과 기대금액의 효용이 동일"한 경우이다.
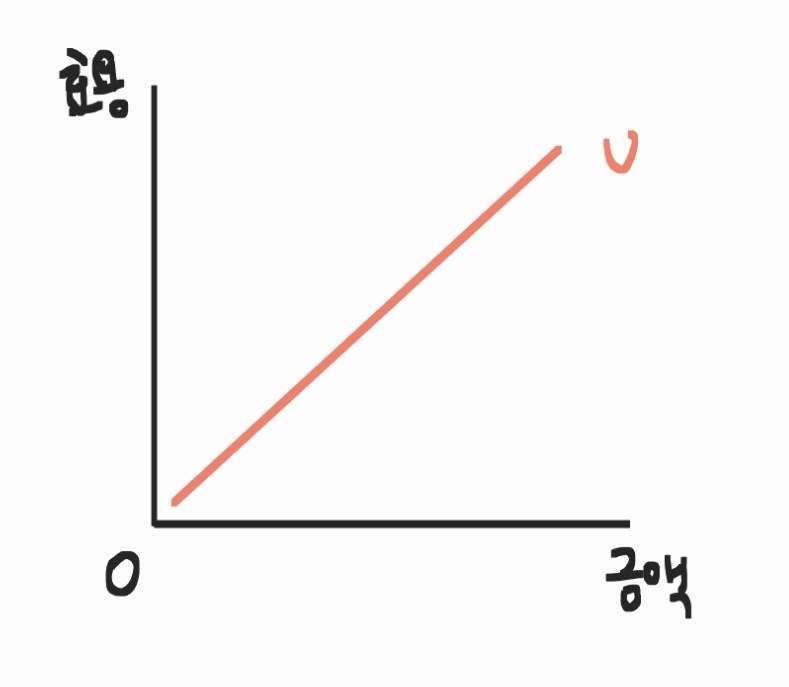
셋째는 '위험선호자'이다.
위험이 재화로 표현되며, "기대효용이 기대금액의 효용보다 큰 경우" 위험선호자라고 한다.

위험태도에 따른 예시 : 보험
소비자의 위험에 대한 태도는 다양한 상황에 적용될 수 있다.
하지만 가장 눈에 띄게 보이는 예시는 바로 보험이다.
미래에 대한 불확실성에 대한 준비로 여겨지는 보험을 통해서 소비자의 선택은 확연하게 드러난다.
대학에서는 보험경제학이라는 수업이 있을 정도로 보험에 대한 경제학적 의미는 상당하다.
보험의 예를 통해서 한번 들여다보자고 할 때 개인에 대한 상황을 가정해보자.
먼저 분석하고자하는 소비자가 '위험기피자'이고, 화재보험에 대한 보험을 가입하고자 한다.
소비자에게는 화재가 발생할 수도 있고, 발생하지 않을 수도 있다.
만약 화재가 발생한다면 나의 재산은 200만원이고, 발생하지 않으면 1,000만원이다.
화재가 발생할 확률은 1/4이라고 하고 보험가입 후 화재 발생시 800만원을 보험금으로 지급하는 보험이 제공된다고 하자.
이런 상황에서 이 소비자의 효용함수는 아래와 같이 그려질 것이다.
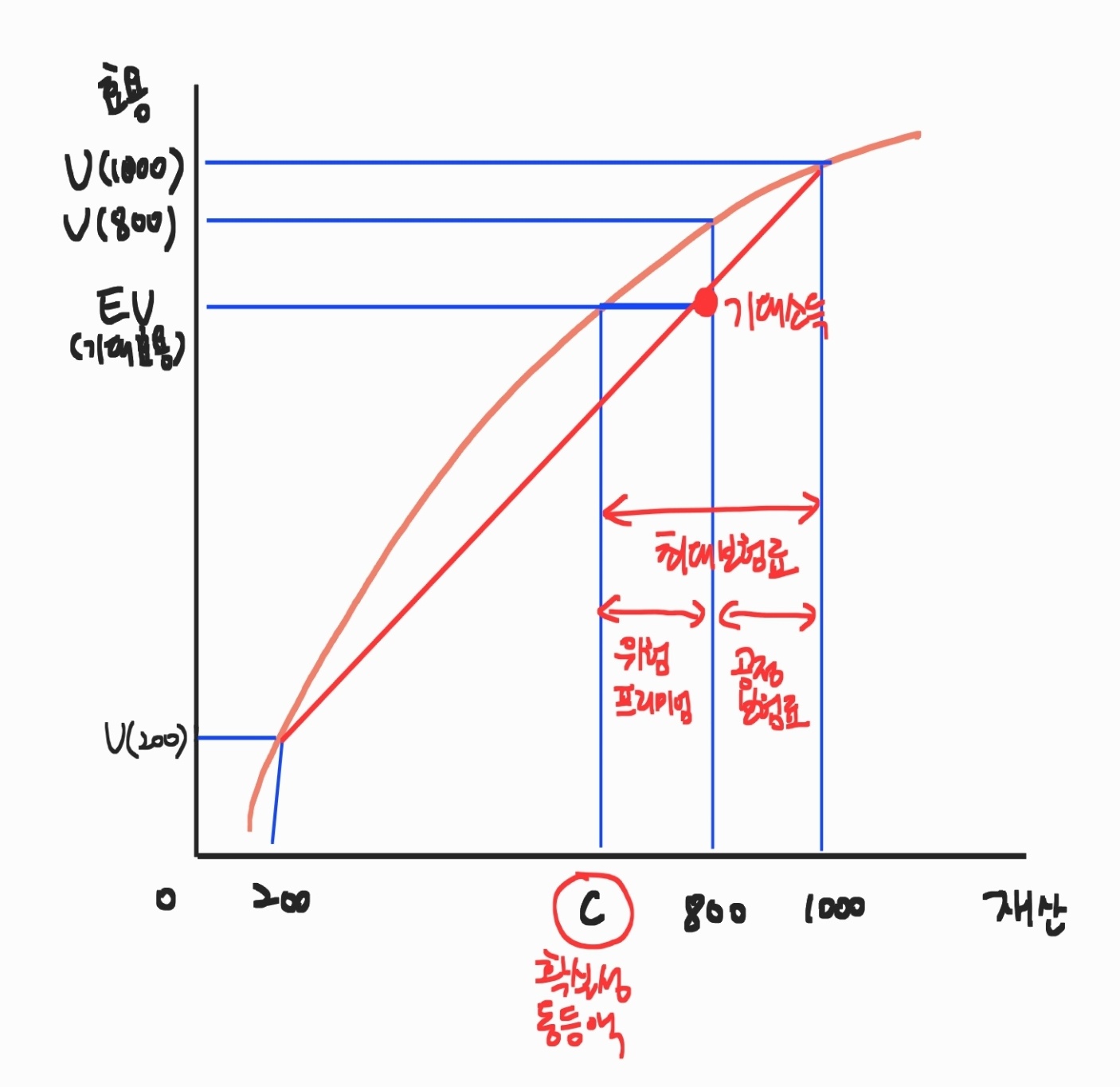
불확실한 상태에서 누리는 기대효용인 EU와 동일한 효용을 가져다주는 확실한 금액을 확실성 동등액이라고 하며 위 빨간색 동그라미로 효시된 C로 나타난다.
사고가 나지 않았을 경우인 1,000만원의 재산과 사고가 났을 경우 받는 보험금 800만원을 공정보험료로 책정된다.
확실성 동등액인 C에서 사고 발생시 수령할 800만원을 위험 프리미엄으로 책정된다.
여기서 소비자가 최대한 낼 수 있는 보험료는 공정보험료와 위험프리미엄의 총 합계이다.
이러한 상황에 대한 설명과 직관적인 소비자 태도로 비교해 보자면,
위험 기피자인 사람은 공정한 보험에 반드시 가입할 것이고, 위험 선호적인 사람은 공정한 보험에 가입하지 않을 것이다.
물론 위험 중립적인 사람은 보험을 가입하든 하지 않든 무던할 것이다.
이렇듯 소비자의 심리는 주변 상황과 개인의 성향에 따라서도 달라질 수 있다.
소비자의 심리는 매우 복잡하고 다양한 것임을 우리는 또 한번 깨닫게 된다.
'경제 이야기' 카테고리의 다른 글
| 기업과 생산비용 : 비용함수 도출 (0) | 2023.09.07 |
|---|---|
| 기업과 생산기술 등 생산이론을 통한 생산함수 (0) | 2023.09.04 |
| 소비자선택이론의 응용 (0) | 2023.08.31 |
| 소비함수이론2 : 생애소득가설, 항상소득가설, Random Walk 가설 (0) | 2023.08.28 |
| 소비함수이론1 : 절대소득가설, 쿠즈네츠 실증분석, 상대소득가설 (0) | 2023.08.28 |



